项目介绍
源代码: https://github.com/VonSdite/K-Means
使用前记得先安装相关的包
1 | pip install -r requirement.txt |
以本项目为例
- 先运行
dataClean.py程序, 对数据iris.data做处理, 得到iris.csv以及真实的分类图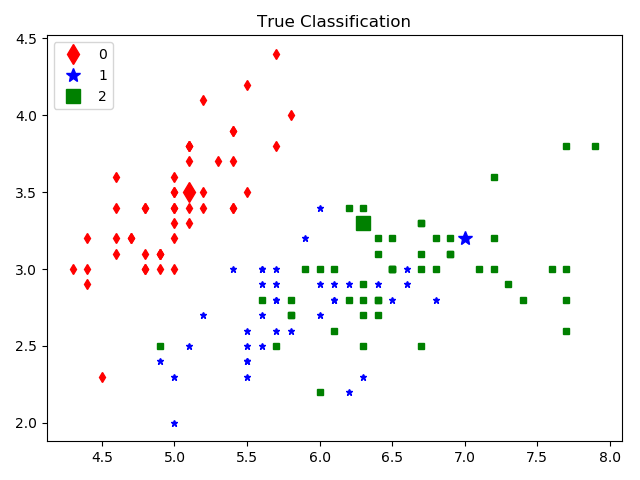
iris.data是鸢尾花数据集, 包含3个不同品种的鸢尾花(Setosa, Versicolour, and Virginica)数据, 以及花瓣和萼片的长度、宽度。 数据有150行4列, 150行指150朵花, 4列分别是Sepal Length(萼片长度), Sepal Width(萼片宽度), Petal Length(花瓣长度) and Petal Width(花瓣宽度)
- 运行
main.py
- 点击
打开-open file, 打开csv文件(也只能打开csv文件)
注意csv文件的要求:
- 要带有表头
- 数据是两列数值数据, 所以需要先处理数据
数据格式类似如下
1 | x,y |
打开后, 会先绘制出数据的散点图
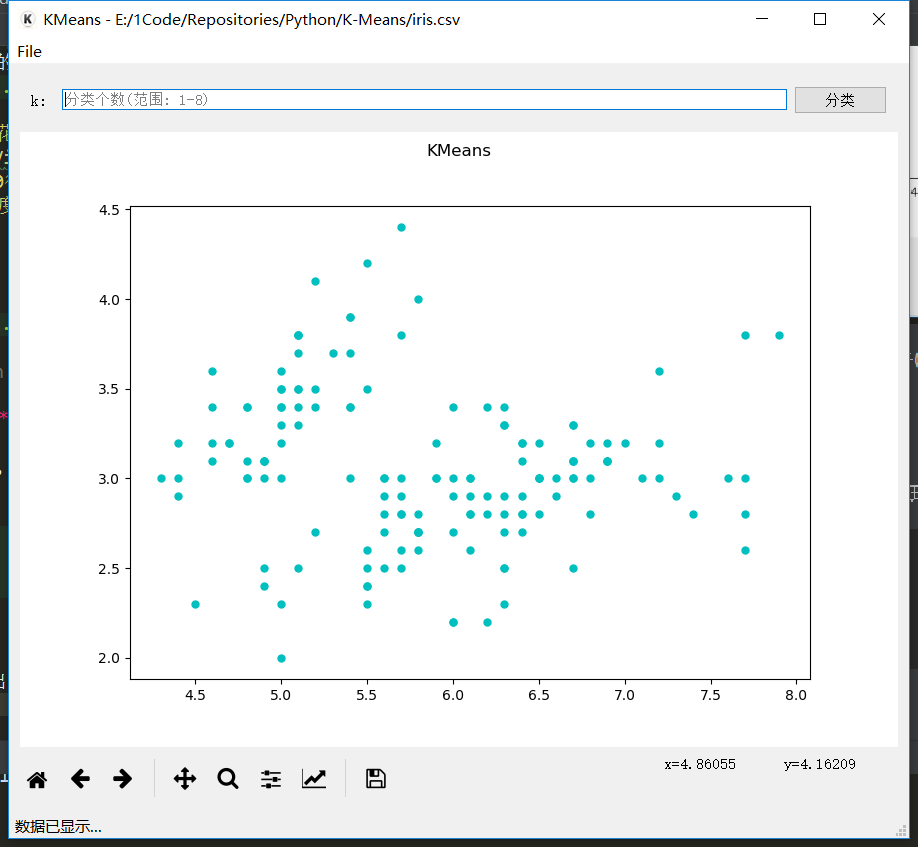
输入
分类个数k-点击分类, 分类过程如下
分类过程中, 左下角状态栏会显示当前的状态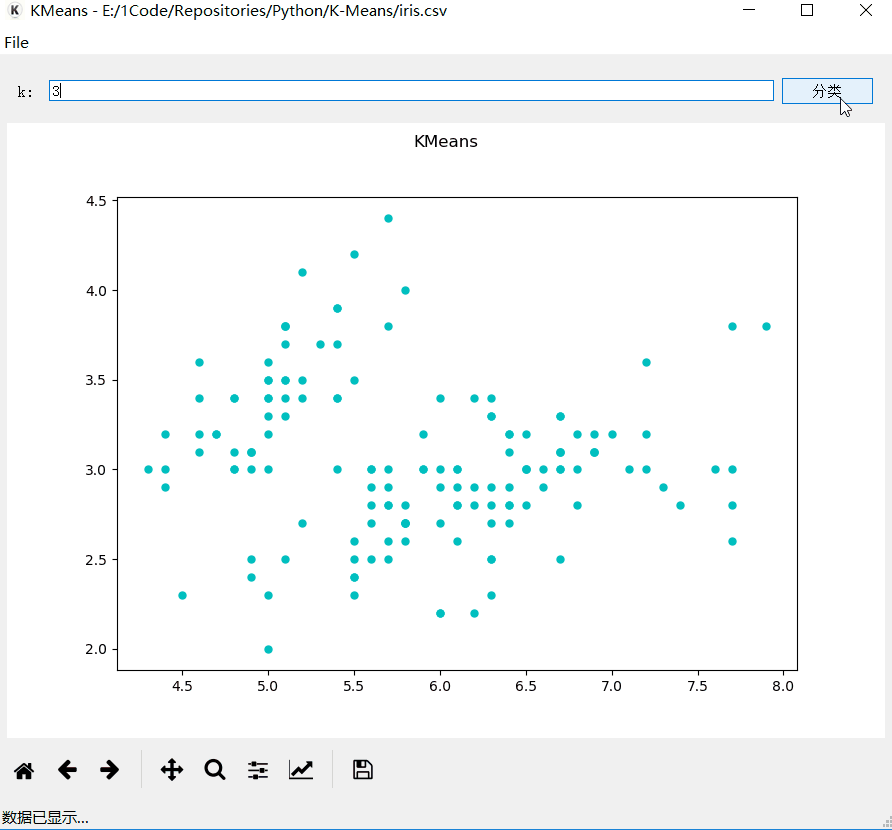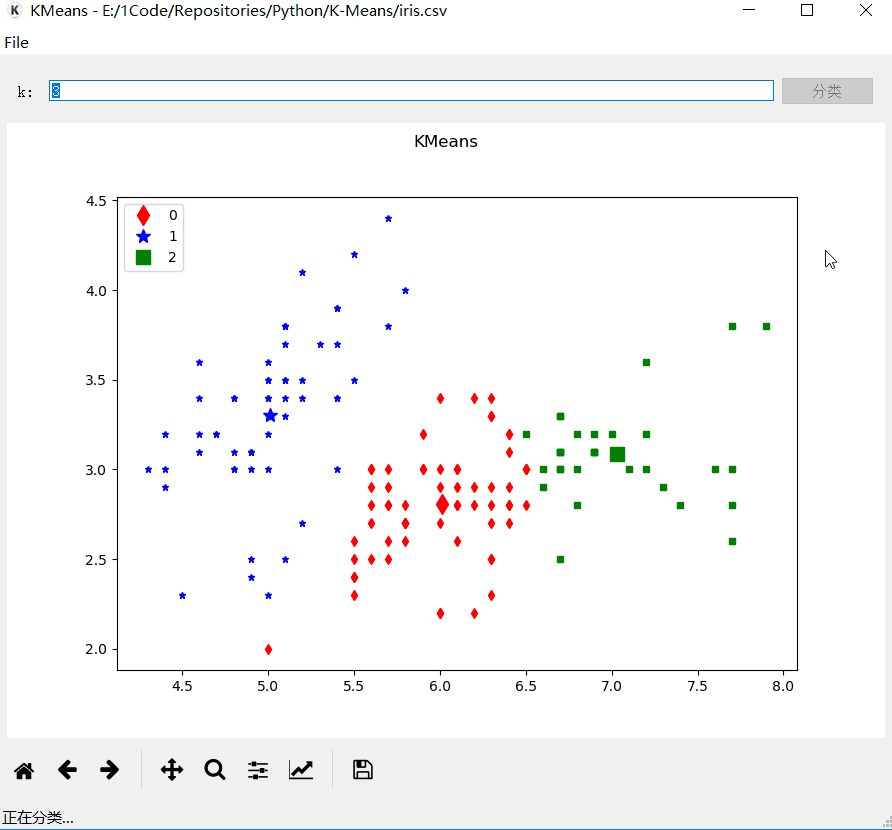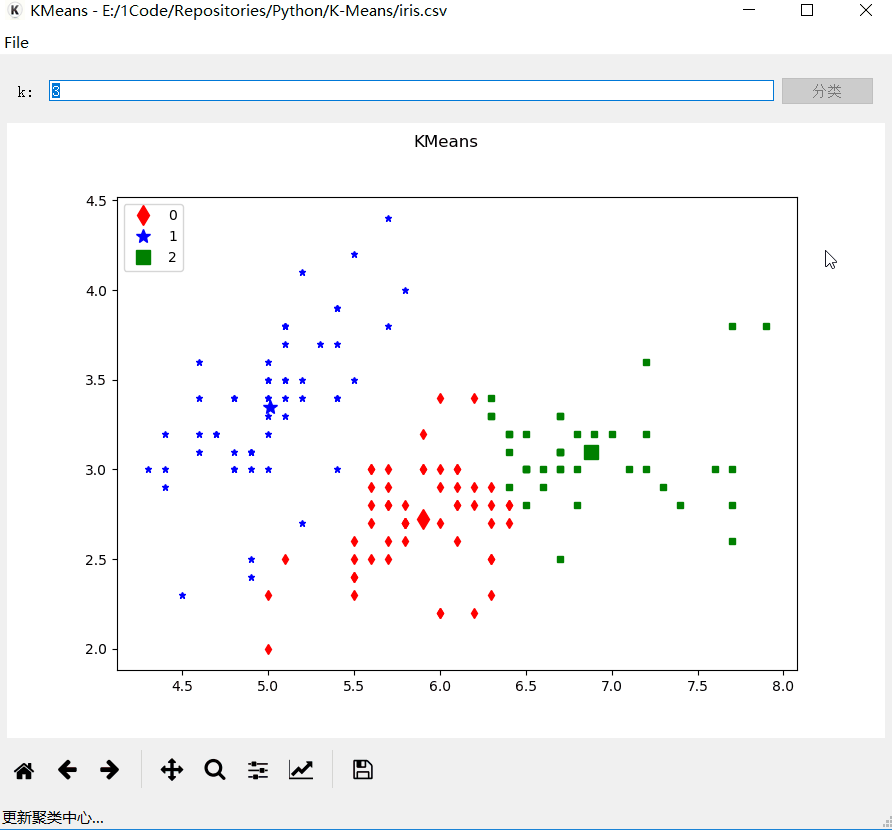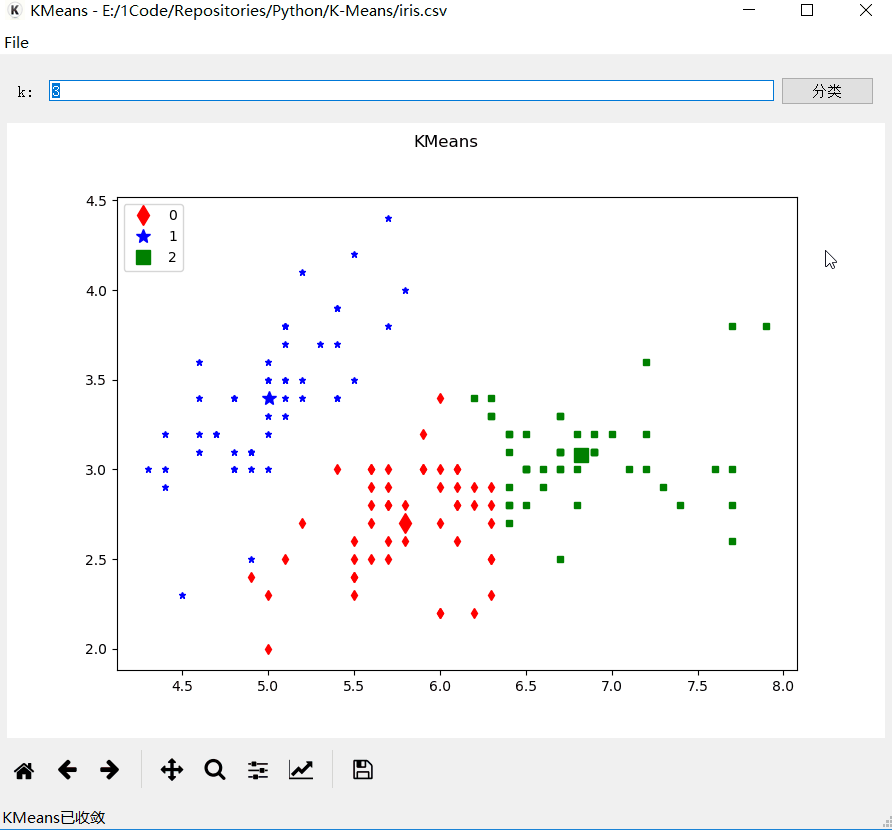
分类结果比较
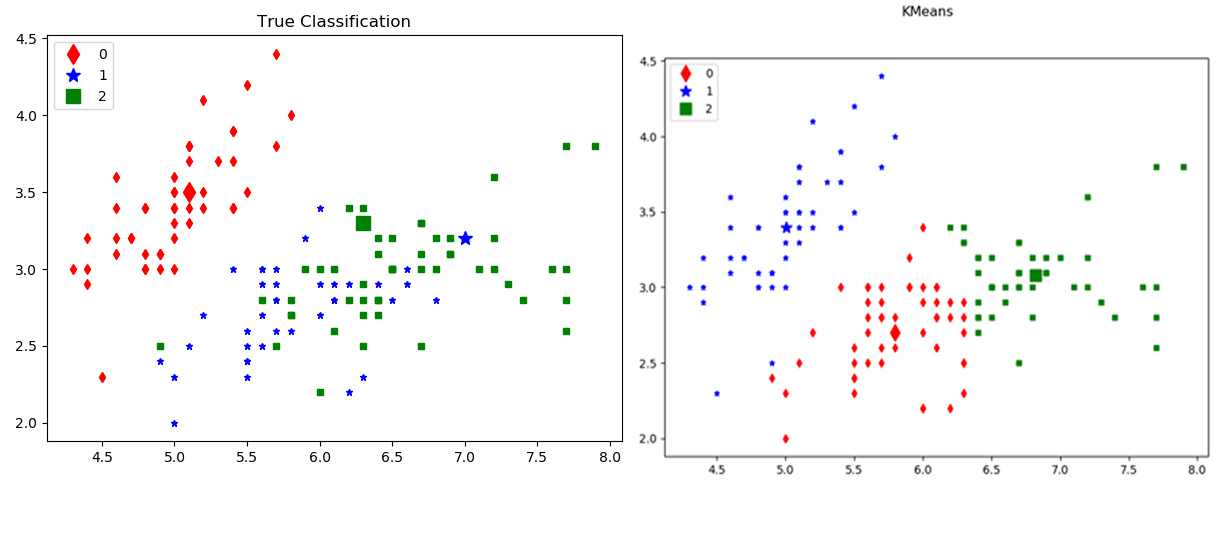
分析
因为数据只用到了萼片的宽度和长度, 只做了二维数据的k-means, 所以对于区分1类和2类花朵的效果还没达到完全区分的效果, 但是已经能万全区分0类花朵了
提升方面, 提升维度, 把花瓣的宽度和长度也考虑进去, 可能可以更好的区分
K-Means介绍
概述
K-means算法是集简单和经典于一身的基于距离的聚类算法
采用距离作为相似性的评价指标, 即认为两个对象的距离越近, 其相似度就越大。
该算法认为类簇是由距离靠近的对象组成的, 因此把得到紧凑且独立的簇作为最终目标。
核心思想
通过迭代寻找k个类簇的一种划分方案, 使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。
k个聚类具有以下特点:各聚类本身尽可能的紧凑, 而各聚类之间尽可能的分开。
k-means算法的基础是最小误差平方和准则,
其代价函数是: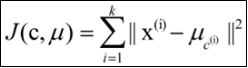 式中, μc(i)表示第i个聚类的均值。
式中, μc(i)表示第i个聚类的均值。
各类簇内的样本越相似, 其与该类均值间的误差平方越小, 对所有类所得到的误差平方求和, 即可验证分为k类时, 各聚类是否是最优的。
上式的代价函数无法用解析的方法最小化, 只能有迭代的方法。
算法实现步骤
k-means算法是将样本聚类成 k个簇(cluster), 其中k是用户给定的, 其求解过程非常直观简单, 具体算法描述如下:
随机选取 k个聚类质心点
重复下面过程直到收敛 {
对于每一个样例 i, 计算其应该属于的类:
对于每一个类 j, 重新计算该类的质心: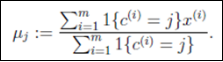
}
其伪代码如下:
1 | 创建k个点作为初始的质心点(随机选择) |
K-means算法补充
K-means算法的缺点及改进方法
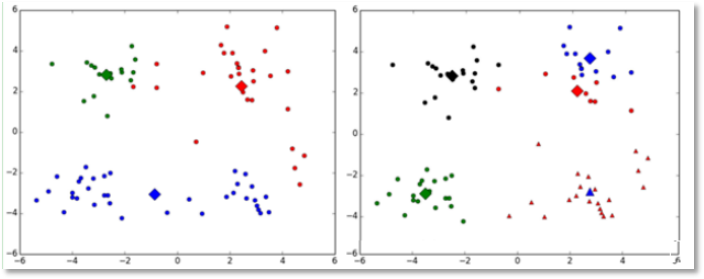
(1)k值的选择是用户指定的,不同的k得到的结果会有挺大的不同,如下图所示,左边是k=3的结果,这个就太稀疏了,蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果,可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的:
改进:
对k的选择可以先用一些算法分析数据的分布,如重心和密度等,然后选择合适的k
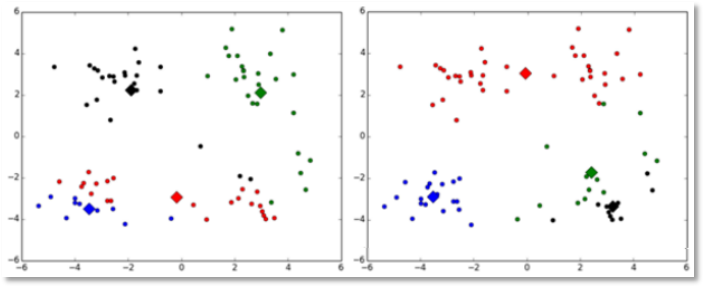
(2)对k个初始质心的选择比较敏感,容易陷入局部最小值。例如,我们上面的算法运行的时候,有可能会得到不同的结果,如下面这两种情况。K-means也是收敛了,只是收敛到了局部最小值:
改进:
有人提出了另一个成为二分k均值(bisecting k-means)算法,它对初始的k个质心的选择就不太敏感
(3)存在局限性,如下面这种非球状的数据分布就搞不定了:
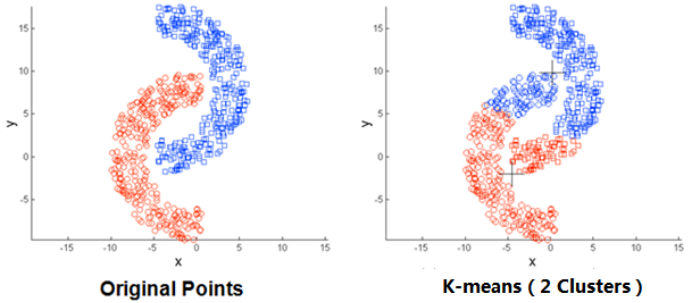
(4)数据集比较大的时候,收敛会比较慢。

